Scheduling and Optimization
Due to the time constraints and high effort required for data acquisition the optimisation of project duration, cost, resource utilization etc. is often severely restrained and therefore a considerable potential for improvement is wasted. This is particularly important during the preparation stage of bids and initial project planning where data is often unreliable or fundamentally incomplete, even though some of that data may already reside in other systems.
Topgallant® Scheduling provides the functionality to address such needs. After defining tasks (using the task definition functionality within the Project Planning solution, possibly employing the Requirements Engineering product) a schedule can be automatically derived considering task constraints such as predecessor/successor relations and duration. Via access to various data sources the optimisation component can be supplied with further relevant input data such as resource capacities and material availability.
Since optimisation results can be produced in minutes, schedules can be updated at any time, e.g. daily or weekly.
Larger/longer projects offer a higher optimisation potential. Examples where several projects having interdependencies and using a pool of constrained resources have shown that the initial duration of typical ship repair projects can be reduced by more than 30% at constant cost level.
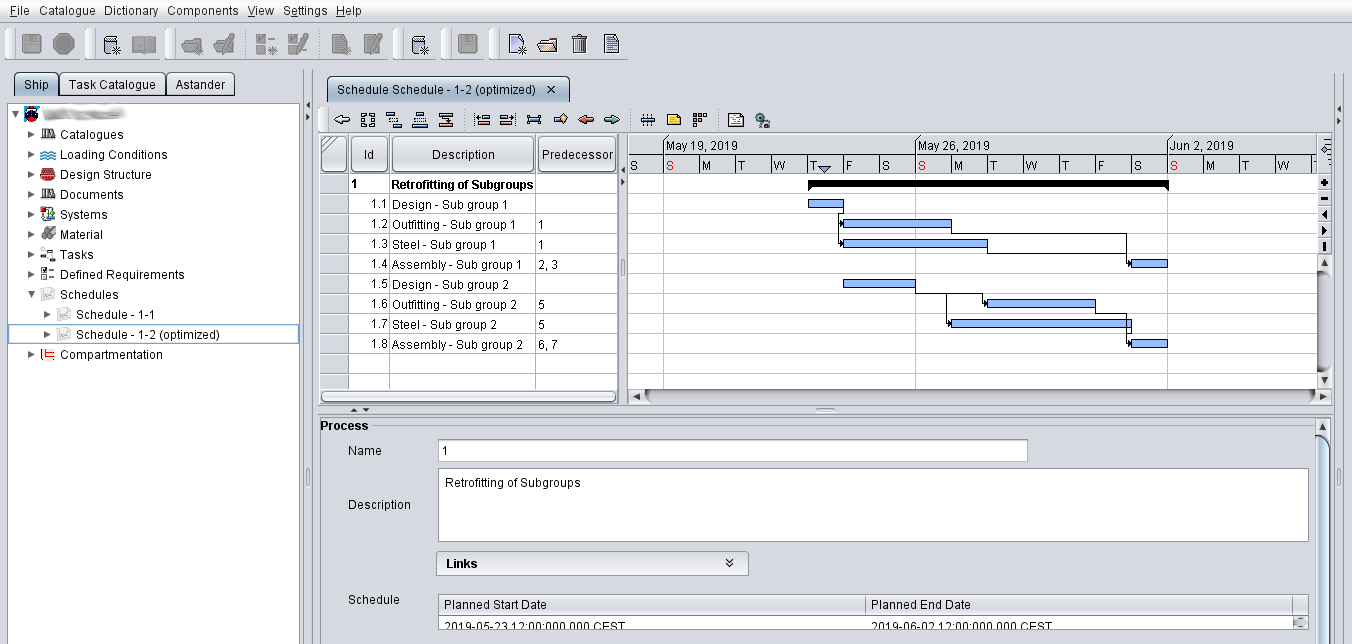
The report generation functionality of Topgallant® Scheduling will help to provide all relevant information such as optimised task structure, schedule, durations, utilization and cost in order to generate documentation for an offer or to transfer such information to project execution stages.
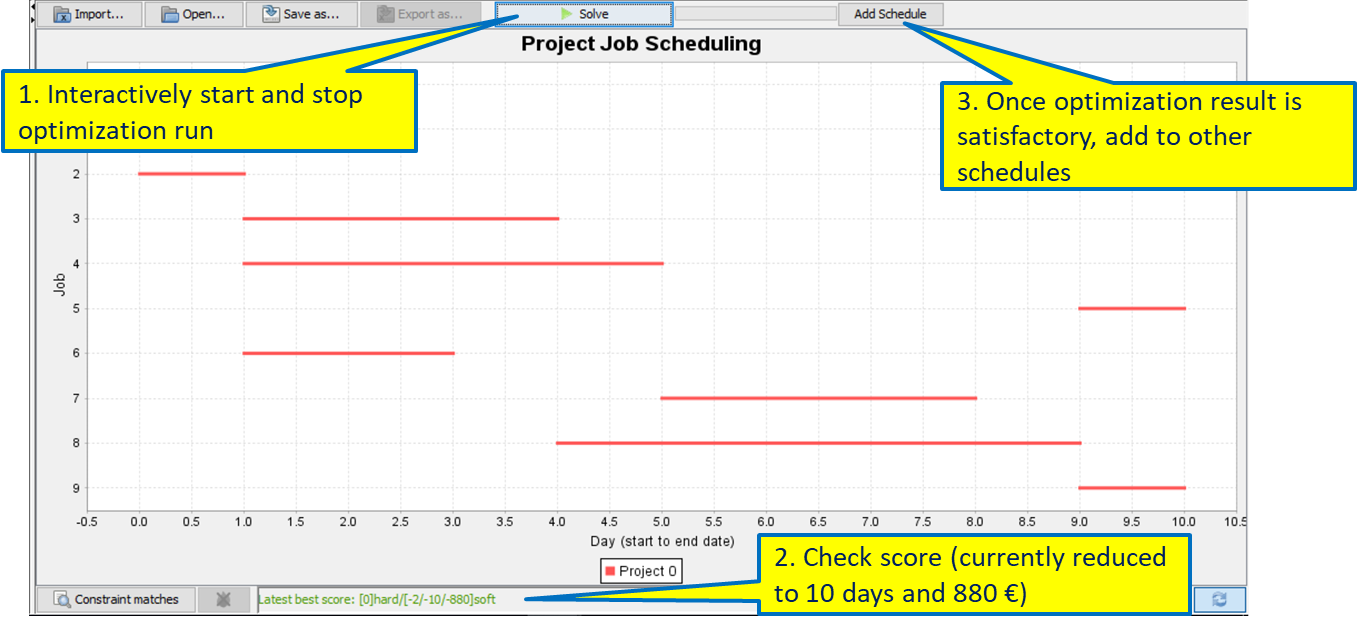
The schedule optimisation component derives optimised solutions, considering a variety and combination of goals such as:
- shortest project execution time
- limited or levelled resources
- best utilization
- lowest cost
or combinations thereof.
An optimised solution for the selected goal is found by variation of:
- the sequence of tasks
- the level of resources for each task
- the resources and related costs
